https://www.acmicpc.net/problem/5676
5676번: 음주 코딩
각 테스트 케이스마다 곱셈 명령의 결과를 한 줄에 모두 출력하면 된다. 출력하는 i번째 문자는 i번째 곱셈 명령의 결과이다. 양수인 경우에는 +, 음수인 경우에는 -, 영인 경우에는 0을 출력한다.
www.acmicpc.net
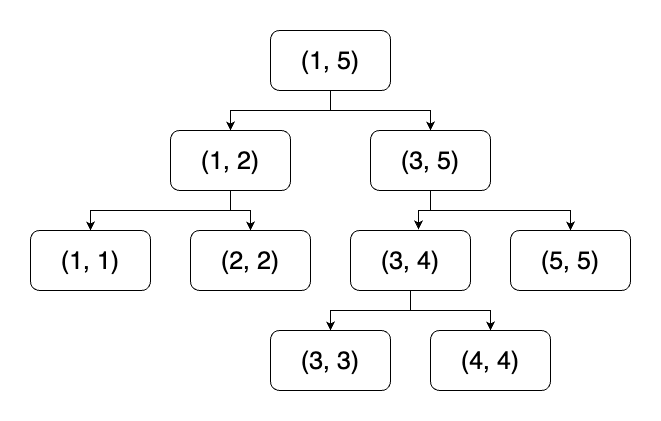
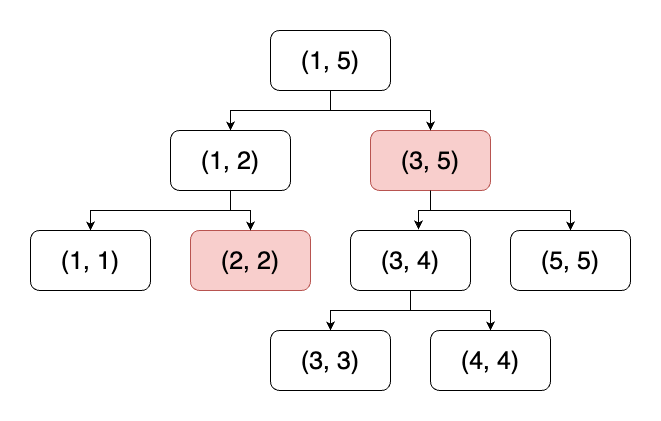
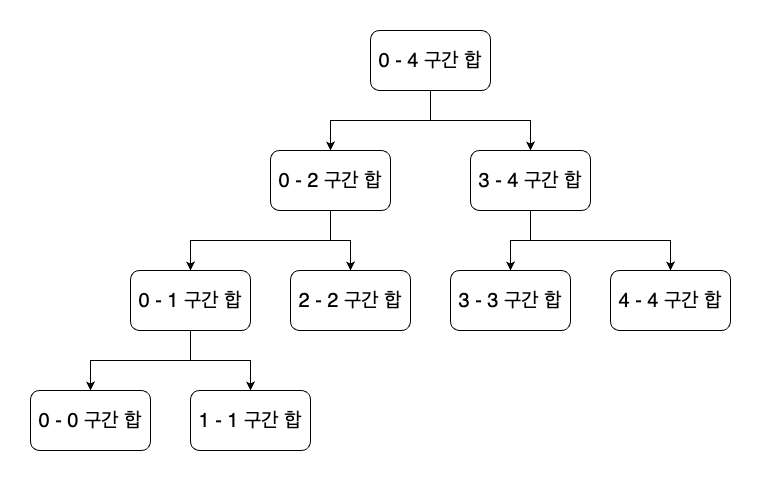
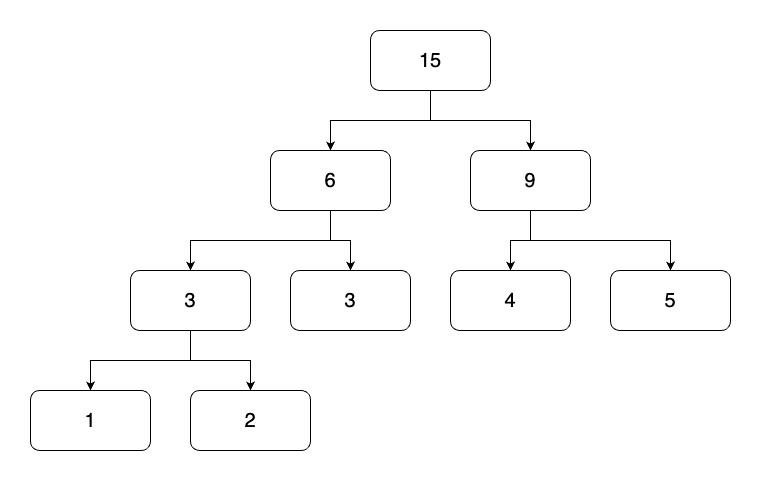
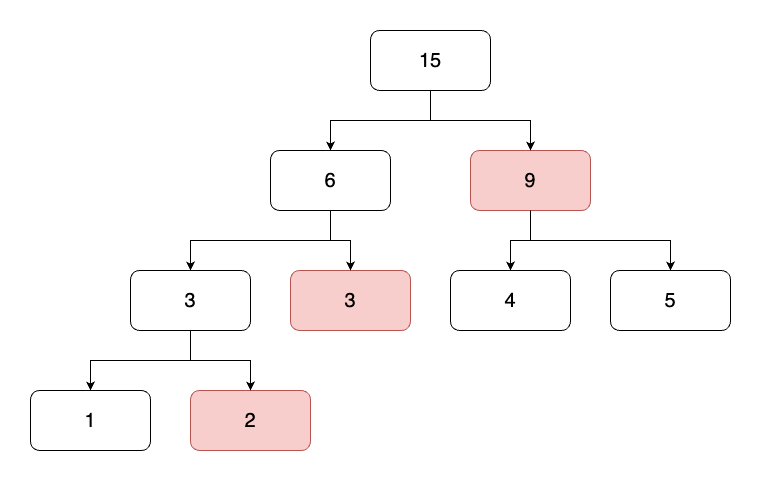
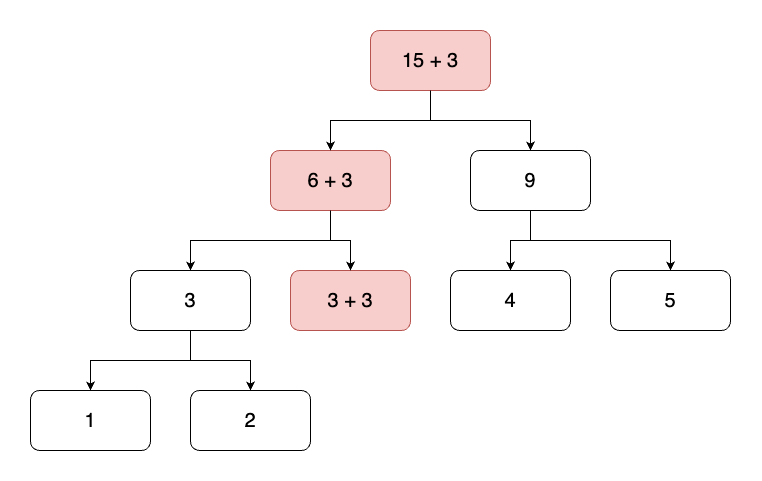
세그먼트트리 문제다.
풀이
단순히 구간 곱 구하기 문제처럼 구하게 된다면 100¹⁰⁰⁰⁰⁰의 수를 담아야 하기에 오버플로우가 발생한다. 즉 해당 문제는 음수, 양수, 0인지 구하면 되는 문제이기에 입력되는 수를 1,0,-1 만으로 트리를 구성하여 결과를 출력하면 된다. 처음 문제를 읽었을 때 입력되는 수를 100 * 10⁵으로 판단하여 일반적인 구간 곱 형태의 트리로 접근하였다가 오답판정을 받았다.
정답 코드

'Problem Solving > BOJ' 카테고리의 다른 글
| [3745] 오름세 (0) | 2023.02.26 |
|---|---|
| [12837] 가계부 (Hard) (0) | 2023.02.23 |
| [18436] 수열과 쿼리 37 (0) | 2023.02.21 |
| [14438] 수열과 쿼리 17 (0) | 2023.02.20 |
| [1306] 달려라 홍준 (0) | 2023.02.18 |