https://www.acmicpc.net/problem/14428
14428번: 수열과 쿼리 16
길이가 N인 수열 A1, A2, ..., AN이 주어진다. 이때, 다음 쿼리를 수행하는 프로그램을 작성하시오. 1 i v : Ai를 v로 바꾼다. (1 ≤ i ≤ N, 1 ≤ v ≤ 109) 2 i j : Ai, Ai+1, ..., Aj에서 크기가 가장 작은 값의 인
www.acmicpc.net
세그먼트 트리 문제다.
풀이
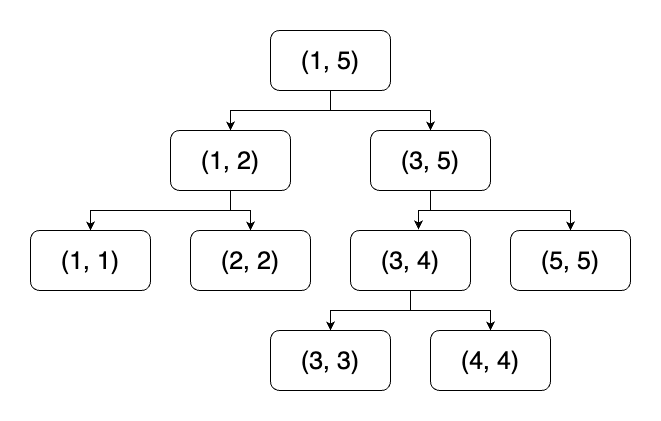
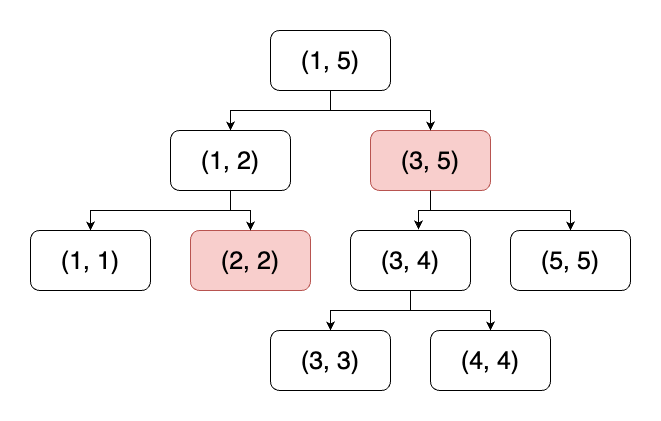
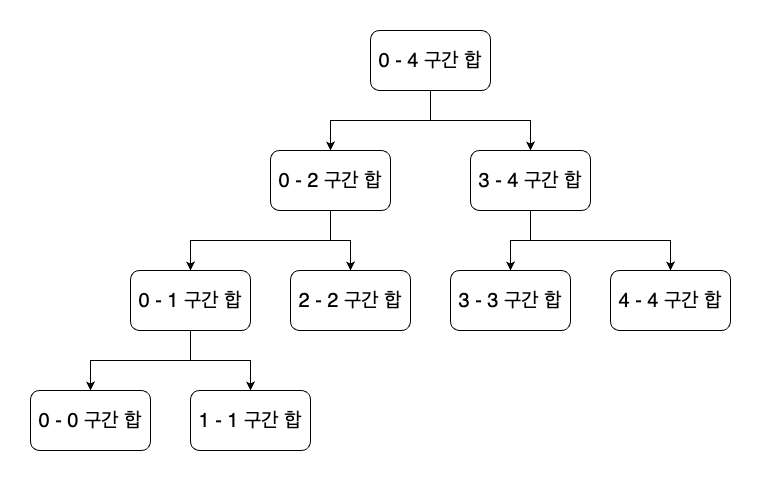
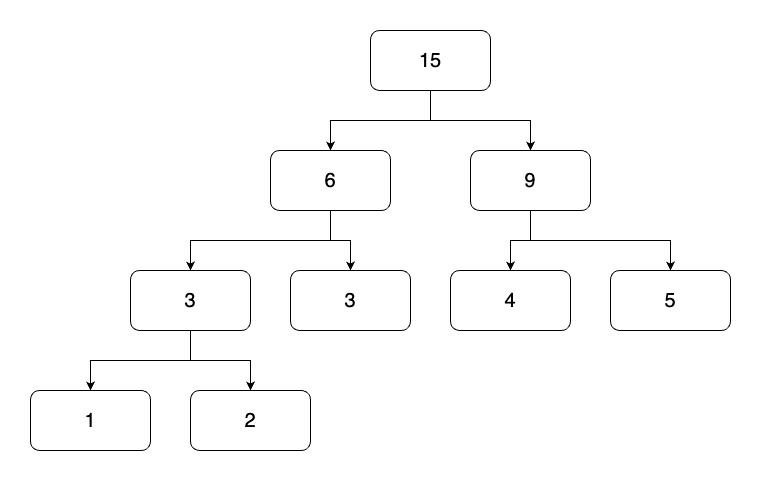
기본적인 세그먼트 트리 문제다. 단, 이번에는 인덱스를 반환하는 것이 목적이므로, 각 노드에는 인덱스가 담기고, 노드의 값은 수열의 값을 비교하여 담아주면 된다.
트리의 값을 읽어올 때, 인덱스가 1부터 시작하므로 수열의 맨 앞에 입력 가능한 범위 밖의 값인 1,000,000,001을 담는다. 이후 범위 밖의 값을 조회하게 될 때 0번 인덱스를 반환하여 대소비교에 영향을 주지 않게 한다.
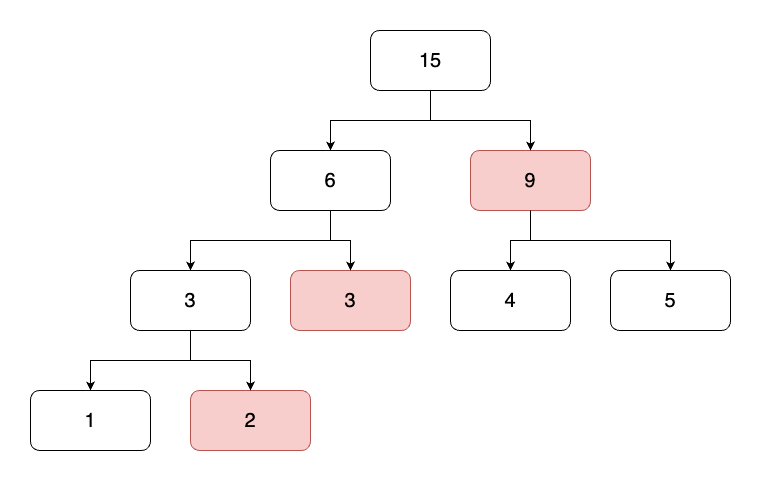
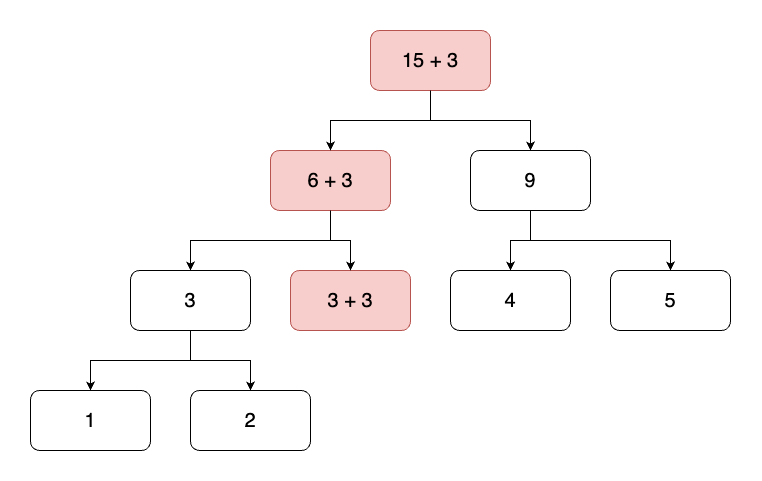
트리의 갱신은 지난번 구간 곱 구하기 문제와 동일하게 수열의 값을 먼저 갱신한 뒤 정해진 구간 내의 리프노드부터 루트노드까지 트리의 갱신을 시도하면 된다.
정답 코드

'Problem Solving > BOJ' 카테고리의 다른 글
| [14438] 수열과 쿼리 17 (0) | 2023.02.20 |
|---|---|
| [1306] 달려라 홍준 (0) | 2023.02.18 |
| [11505] 구간 곱 구하기 (0) | 2023.02.16 |
| [2357] 최솟값과 최댓값 (0) | 2023.02.15 |
| [2042] 구간 합 구하기 (0) | 2023.02.15 |