https://www.acmicpc.net/problem/11054
11054번: 가장 긴 바이토닉 부분 수열
첫째 줄에 수열 A의 크기 N이 주어지고, 둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ N ≤ 1,000, 1 ≤ Ai ≤ 1,000)
www.acmicpc.net
동적계획법으로 접근 가능한 문제다.
풀이
크기 A인 두 개의 dp 배열을 만든다. 하나는 0부터 해당 인덱스까지 증가하는 부분수열의 최대 개수, 다른 하나는 A-1번부터 해당 인덱스까지 감소하는 부분수열의 최대개수를 담아내어 ans배열에 두 배열의 값을 합쳐서 최댓값을 계산하면 된다.
i는 0부터 A까지, 즉 구하고자 하는 대상의 인덱스, k는 0부터 i까지 즉 처음부터 자기 앞번호까지의 원소를 순회할 때 점화식은 다음과 같다.
if arr[k] < arr[i]
dp[i] = max(dp[i], dp[k]+1)
즉 자신보다 작은 원소로 끝나는 증가하는 부분 수열에 원소 i를 붙이기만 하면 해당 원소로 끝나는 증가 부분 수열이 완성되기에 해당 조건 내에서 최댓값으로 갱신하면 답을 구할 수 있는 것이다. 예제를 기준으로 구한 dp 배열은 다음과 같다.

감소하는 부분수열의 경우는 해당 배열을 역순으로 탐색하면 구할 수 있다. 주의할 점은 증가하는 부분수열의 개수에서 자기 자신을 포함하여 계산했기에 1로 초기화했으나 감소하는 부분수열은 자기 자신을 포함하지 않은 0으로 초기화해야 중복을 피할 수 있다.
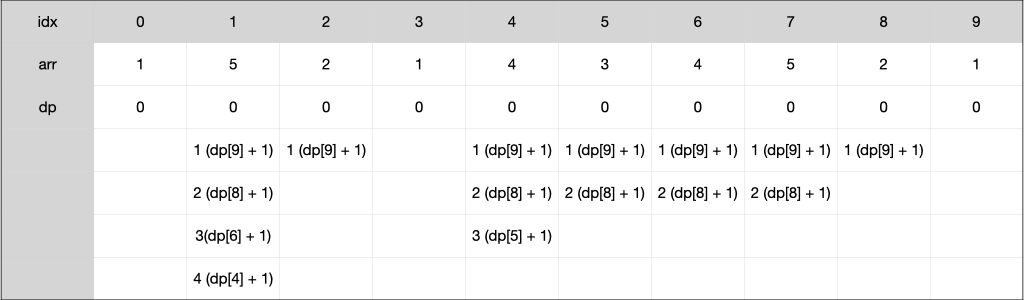
마지막에는 해당 배열의 총합을 더하여 최댓값을 출력해 주면 된다.
정답 코드

'Problem Solving > BOJ' 카테고리의 다른 글
| [2042] 구간 합 구하기 (0) | 2023.02.15 |
|---|---|
| [2533] 사회망 서비스(SNS) (0) | 2023.02.13 |
| [10830] 행렬 제곱 (0) | 2023.02.11 |
| [2638] 치즈 (0) | 2023.02.10 |
| [11779] 최소비용 구하기 2 (0) | 2023.02.10 |